Radiative transfer of leaves

J Gómez-Dans (UCL & NCEO)

j.gomez-dans@ucl.ac.uk

What is radiative transfer theory?

• The properties of the leaves and the canopy are combined
• For analysis, untangle response of the leaves and canopy.
• We want to understand the processes and properties that control sunlight being reflected by an e.g. canopy.
• RT tries to derive a physical description of the fate of photons as they are scattered and absorbed within a canopy.
• Let's start with leaves
• ... then we'll embed them in a canopy.

Modelling leaf optical properties

• Photon hits a leaf, it can be
  • absorbed ($A$),
  • scattered ($R$), or
  • transmitted ($T$).
• From energy conservation $A+R+T=1$
• Implicit dependence on wavelength ($\lambda$)

How does a leaf look like?

Monocot

Dicot

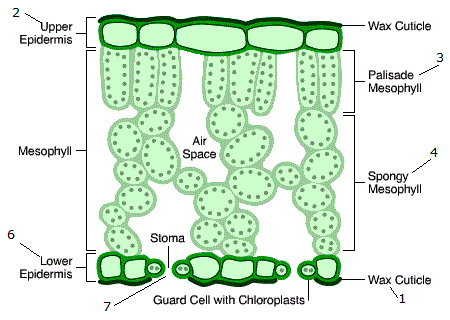
Leaf reflectance: directional aspects

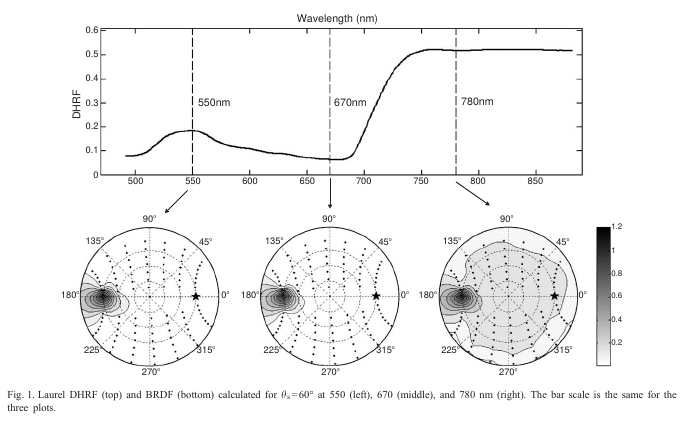
• The wax cuticle is bright, and scatters incoming radiation with a strong directional signal in the specular direction, $R_s$.
• Specular response broadened by the leaf's surface microtopography.
• At interfaces between different materials, photons are scattered.
• Internal contribution $R_d$ is Lambertian (isotropic), the result of photons interacting with internal leaf structure and pigments.

Leaf reflectance: spectral aspects

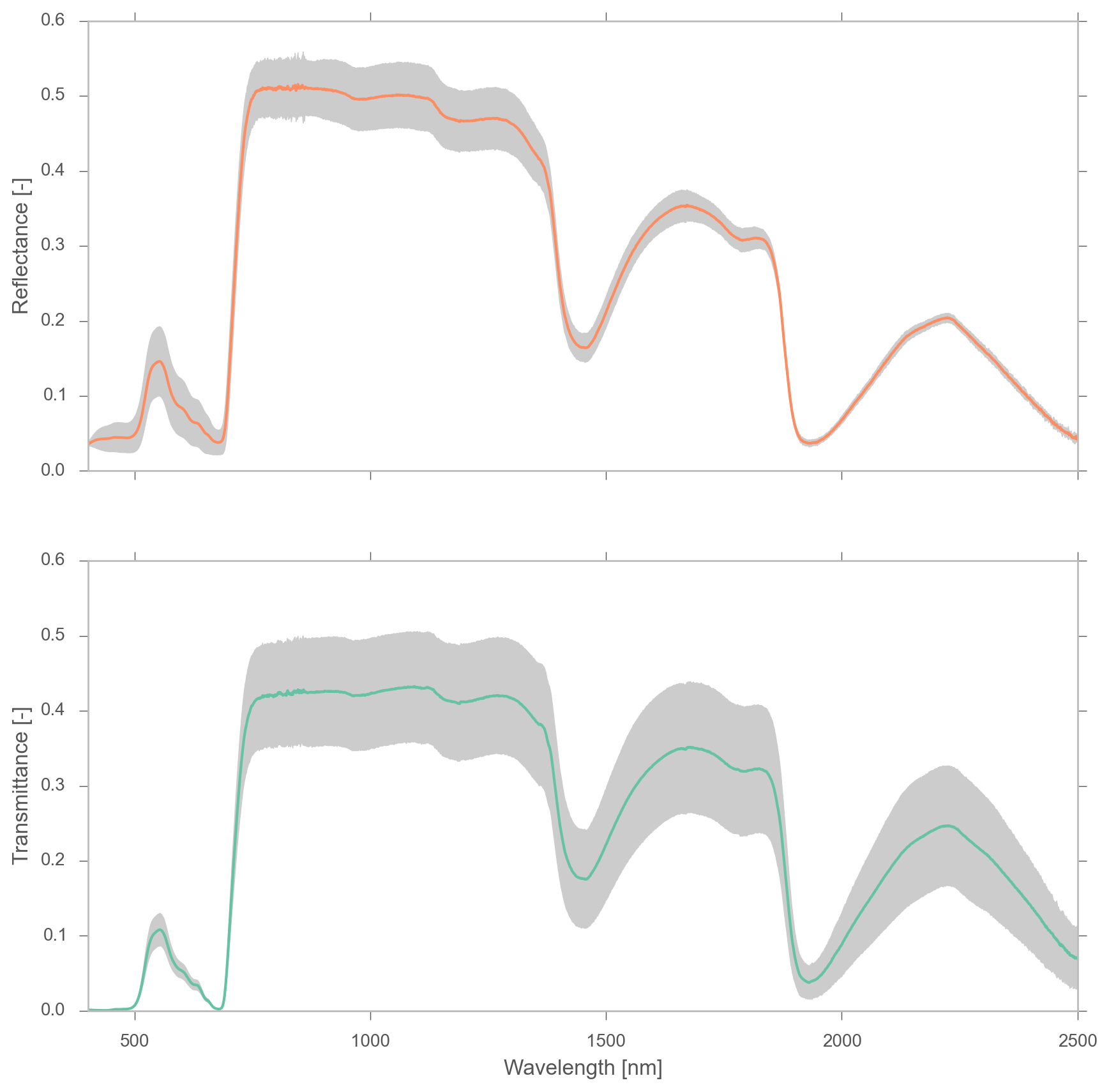Main spectral regions:

1. VIS $[400-700nm]$: absorption of radiation in green leaves. Chlorophyll, carotenoids, ..
2. NIR $[700-1100nm]$: multiple scattering due to air-cell wall interfaces,
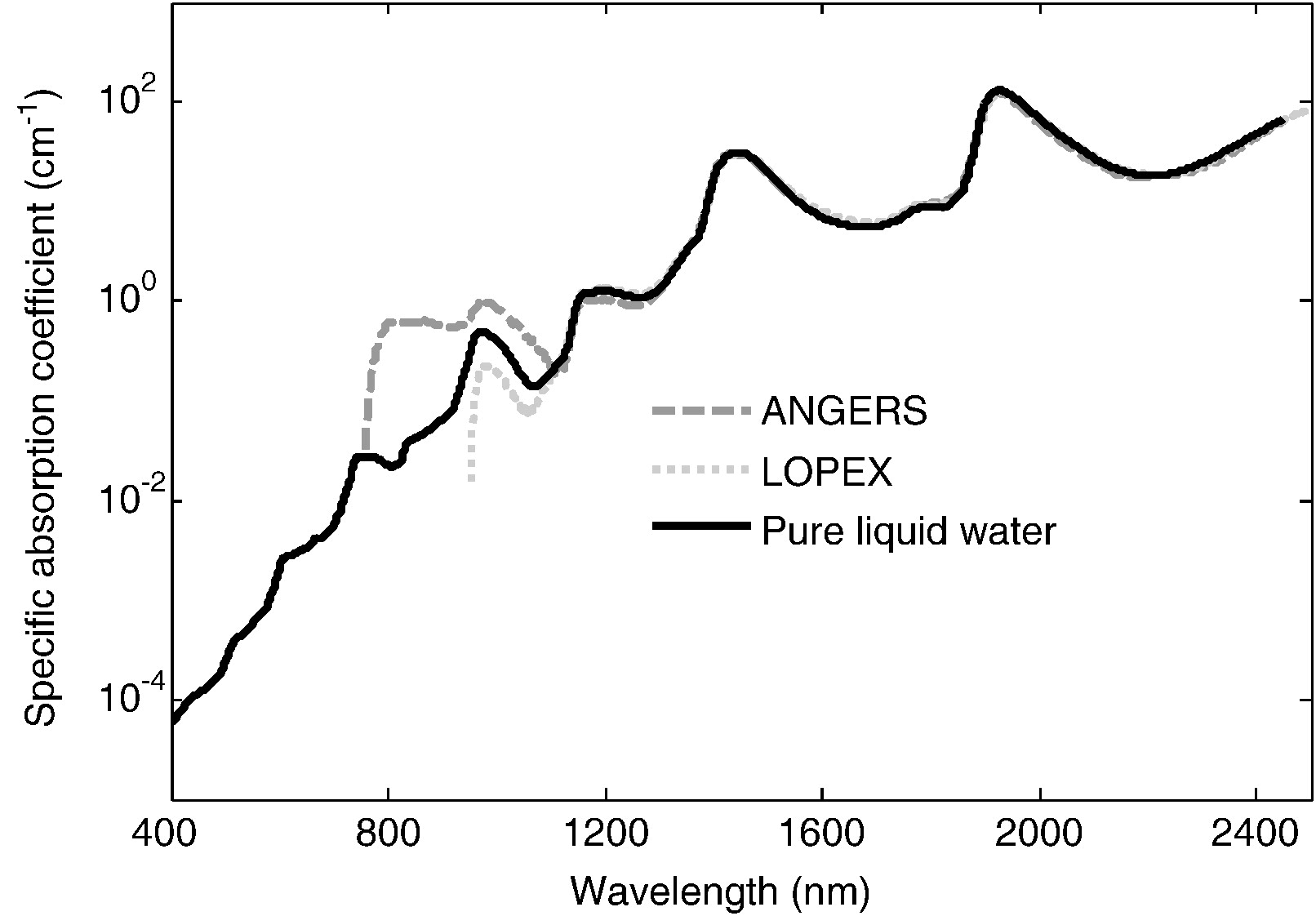
3. SWIR $[>1100nm]$: mostly water absorption, note peaks at 1450, 1950 and 2500 nm.

• We will focus on the Lambertian effect
• This is a consequence of internal photon scattering
• therefore, it should tell us something about the internal structure and composition of the leaf.
• Although specular component is important, it is often neglected!

A simple leaf model

• A monocot leaf looks like a slab

• What's weird about this photo? ;-)

• We can model it by considering the internal reflections of a bean inside a plate:

• Solution to plate model given Airy in 1833, applied to leaves by Allen and others in 1970s
• We can write a fairly compact expression for the reflectance and transmittance of the plate that only depends on
  • The index of reflection of the plate, $n$, and
  • The absorption coefficient $k$.
• The model works surprisingly well for monocots, but fails for more complex leaves or senescent leaves.

A multilayer leaf model

• Numerous photon scatter events take place at the air-cell boundaries within the leaf mesophyll
• So extend model to have a stack of plates separated by air interfaces to account for these interactions

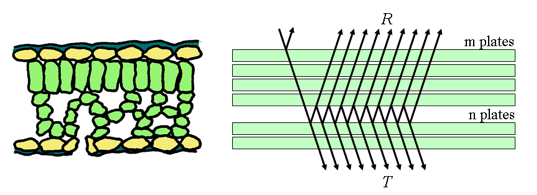
• Problem solved by Stokes in 1862.
• Can calculate leaf reflectance and transmittance of $N$ layers as a function of a single layer ($R(1)$ and $T(1)$):

$$ \frac{R(N)}{b^{N}-b^{-N}}=\frac{T(N)}{a-a^{-1}}=\frac{1}{ab^{N}-a^{-1}b^{-N}}, $$

where

$$ \begin{align} a &=\frac{1+R^{2}(1)-T^{2}(1) + \Delta}{2R(1)}\\ b &=\frac{1-R^{2}(1)+T^{2}(1) + \Delta}{2T(1)}\\ \Delta &= \sqrt { (T^{2}(1)-R^{2}(1)-1)-4R^{2}(1)}. \end{align} $$

• Can make number of layers a real number not an integer (e.g. 1.3 layers)
• $\Rightarrow$ PROSPECT
• PROSPECT predicts leaf reflectance and transmittance as a function of
  • $N$ (the number of layers $\sim \left[1.5-2.5\right]$, a sort of internal complexity of the leaf parameter)
  • Calculates $k$ from the concentrations of
    • Chlorophyll a+b
    • Leaf water
    • "Brown pigment"
    • "Dry matter"
    • Carotenoids

Chlorophyll a+b specific absorption

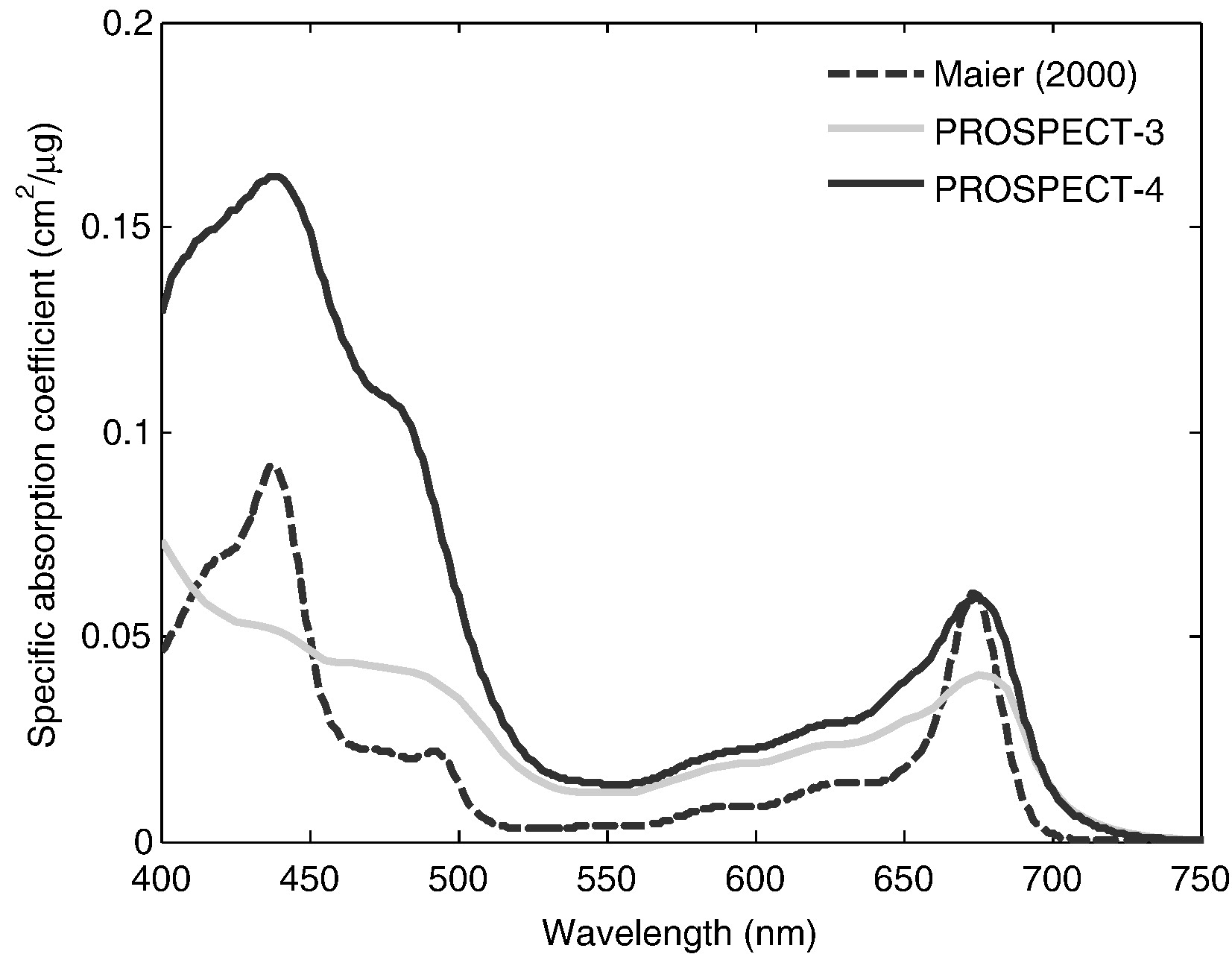
Carotenoids specfic absorption

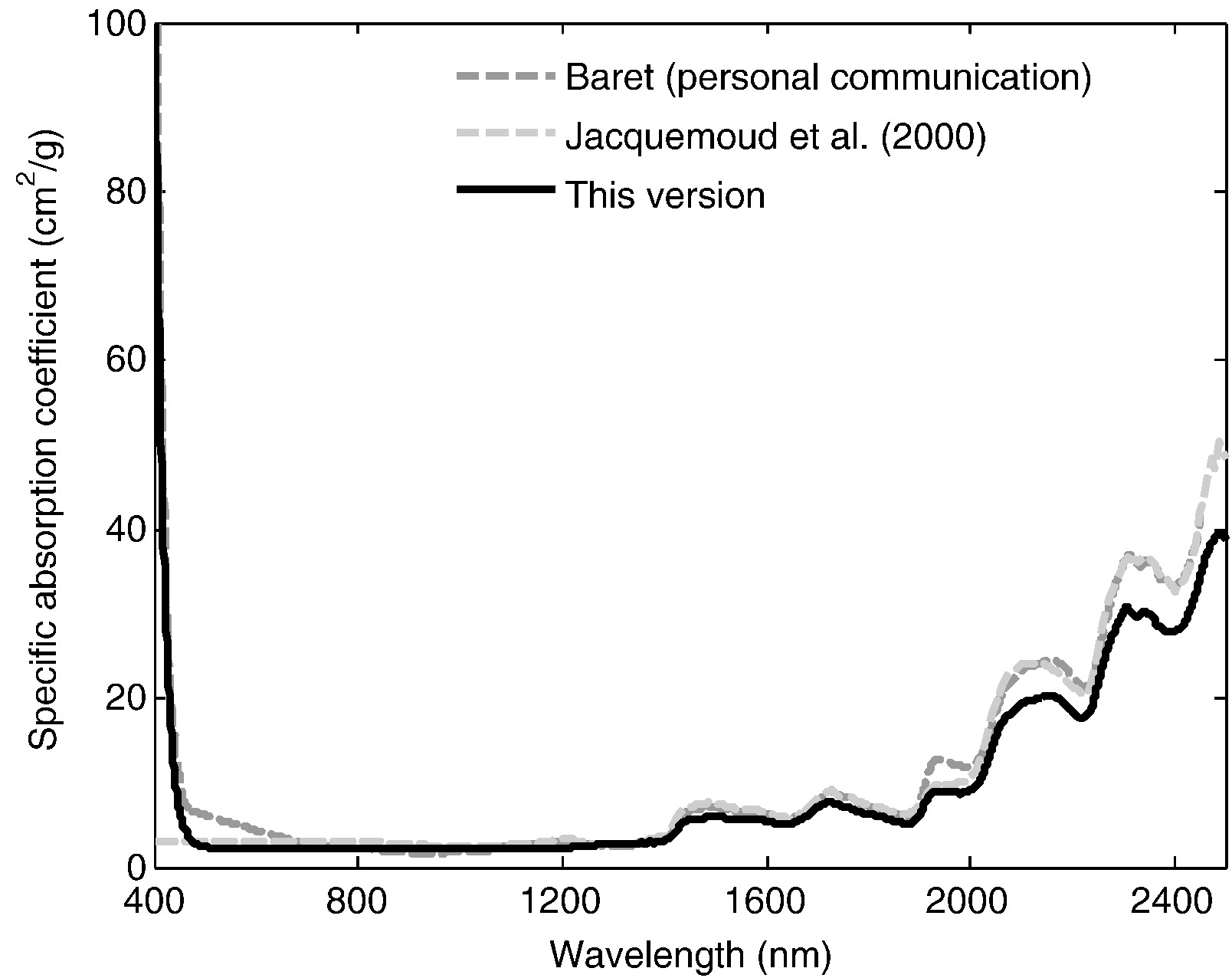
Dry matter specific absorption

Water specific absorption

• Cellulose and lignine as well as proteins have particular absorption fingerprints
• However, absorption coincides with water absorption
• Hence these responses lumped into "Dry matter".

Recap

• Leaf BRDF
  • Directional component due to surface specular reflection
  • Lambertian component due to internal interactions
• Leaves can be modelled as stacks of plates
• Parsimonious model with a handful of parameters
• PROSPECT:
  • N layers ($N\in R$)
  • Chlorophyll concentration $(\mu gcm^{-2})$
  • Carotenoids $(\mu gcm^{-2})$
  • Equivalent water thickness $(cm)$)
  • Dry matter $(gcm^{-2})$